#Rekenfeitje 15 – door Robert Hendriks
De kracht van het drieslagmodel bij het rekengesprek
Als een leerling vaker een rekenfout maakt bij hetzelfde type opgave, hoe kom jij als leraar er dan achter waar die fout in zit? En misschien nog wel belangrijker; hoe krijgt de leerling hier zicht op? Het voeren van een rekengesprek en inzetten van het drieslagmodel kan hierbij helpen. In dit rekenfeitje lees je wat een rekengesprek inhoudt en op welke manier het drieslagmodel daarbij inzicht geeft in het probleemoplossend handelen van de leerling.
Het inzetten van het drieslagmodel
Het rekengesprek is een semi-gestructureerd, dynamisch interview met een proces-georiënteerd karakter (Allsopp et al., 2008; Ginsburg, 2009; Van Luit, 2019) met als doel om denkstrategieën expliciet te maken. Hierdoor leren leerlingen bewuster keuzes maken (Flavell, 1979). Het rekengesprek heeft zowel een doel voor de leraar als voor de leerling. Belangrijk doel voor jou als leraar is het zicht krijgen op de denk- en oplossingsprocessen van de leerling. Voor de leerling geldt dat hij zicht krijgt op eigen handelen, en tools vergaart om in de les te gebruiken.
Het drieslagmodel is een krachtig middel om in te zetten tijdens een rekengesprek. Dit model wordt gebruikt voor het analyseren van probleemoplossend handelen van leerlingen bij contextopgaven (Van Groenestijn, 2002) en biedt aanknopingspunten voor het didactisch handelen van de leraar (Protocol ERWD, Borghouts, van Groenestijn, Janssen, 2011).
Drie vaste stappen bij contextopgaven
Bij het gebruik van het drieslagmodel als onderlegger voor het rekengesprek leg je de focus op de assen. Deze assen representeren de drie vaste uit te voeren stappen bij het oplossen van contextopgaven. Bij elke as kun je vragen stellen.
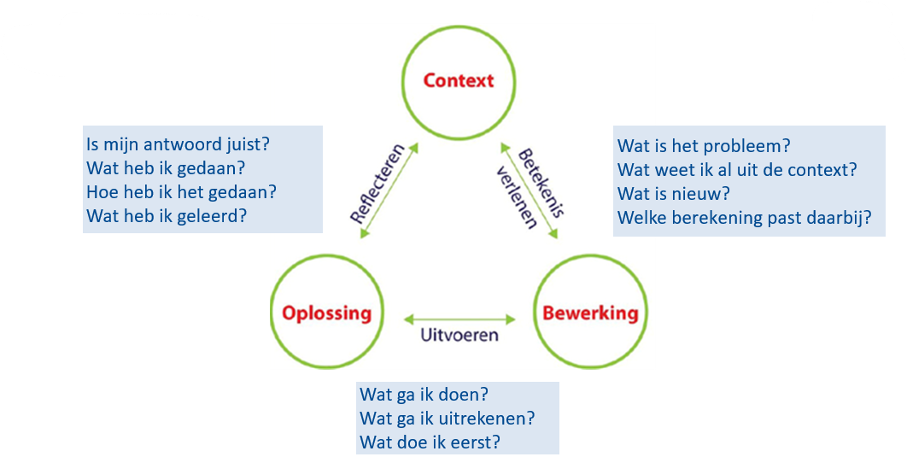
(Protocol ERWD, Borghouts, van Groenestijn, Janssen, 2011)
Bijvoorbeeld:
- Bij de as ‘Betekenis verlenen’: Kan de leerling zelfstandig een verhaal bedenken bij de opgave ‘Bereken 20% van €200,-‘?
- Bij de as ‘Uitvoeren’: Weet de leerling hoe hij hulpstappen kan noteren bij het uitrekenen van een opgave?
- Bij de as ‘Reflecteren’: Kan de leerling na het uitrekenen van de opgave hardop vertellen of laten zien wat hij heeft gedaan?
Het voeren van een rekengesprek blijkt effectief om te achterhalen wat leerlingen nodig hebben bij het leren rekenen, en heeft positieve invloed op leerkrachtfactoren, zoals het handelen tijdens de rekenles (Kaskens, 2022). Het inzetten van het drieslagmodel bij het rekengesprek helpt je om de oorzaak van hardnekkige rekenfouten bij leerlingen te achterhalen. Zo kun je hen vervolgens de juiste tools aanreiken.
 Versterken van het rekenonderwijs
Versterken van het rekenonderwijs
Meer lezen over het versterken van het rekenonderwijs bij jou op school, neem dan een kijkje op onze themapagina!
Rekenfeitjes
Het vakgebied rekenen-wiskunde is enorm groot. Voor leraren kan het dan ook een uitdaging zijn om een goede rekenles te geven. Welke didactiek pas je in welke leerlijn toe? Wat zegt wetenschappelijk onderzoek eigenlijk over leren rekenen in de verschillende domeinen? Met deze rekenfeitjes geven we jou als leraar – kort maar krachtig – wat extra bagage mee. Zodat je in jouw rekenles goed beslagen ten ijs komt.
Ondersteuning van Expertis
Heb je vragen over (de verbetering van) het rekenonderwijs? Neem gerust contact op met onderwijsadviseur Robert Hendriks via 06 – 44 26 24 06 of robert.hendriks@expertis.nl
Meer lezen?
Meer lezen over hoe we samen met scholen werken aan passend rekenonderwijs voor alle leerlingen?

Bronnen
- Flavell, J.H. (1979). Metacognition and cognitive monitoring. A new area of cognitive-developmental inquiry. American Psychologist, 34(10), 906-911.
- Kaskens, J. (2018). Rekengesprekken voeren. Uitgeverij Pica.
- Kaskens, J. (2022). Leren van rekengesprekken. Volgens Bartjens, 42(1), 4-8.
- Kaskens, J. (2022). De rekenontwikkeling en onderwijsbehoeften van leerlingen. Volgens Bartjens, 42(2), 41-53.
- Van Groenestijn, M., Borghouts, C. & Janssen, C. (2011). Protocol Ernstige RekenWiskundeproblemen en Discalculie. BAO SBO SO. Uitgeverij Van Gorcum.
